👏 Deep Neural Networks Run on the Photonic Platform！
💥 Photonic Neural Networks are ultra-fast and dramatically power efficiency.

Confluence of photonics and deep learning embodies the photonic neural networks.

💬 Preface

🎯 This post serves to comprehensively illustrate the theoretical derivations and physical implementations augmenting discussions of my two accepted papers:

1. Yinyi Liu et al. "A Reliability Concern on Photonic Neural Networks." Design, Automation and Test in Europe Conference (DATE). 2022.
2. Yinyi Liu et al. "Reduce the Footprints of Multiport Interferometers by Cosine-Sine Decomposition." Optical Fiber Communication (OFC). 2022.

👨‍💻 The modeling codes are available on my github: Photonic-Neural-Networks. The slides shown in this post are from one of my talks and also archived on my personal website.

🌱 Background

🏃 Ongoing advances in deep learning have enabled researchers in multidisciplinary domains to achieve things that once seemed inconceivable: pedestrian recognition and automatic navigation for self-driving cars, disease diagnosis and drug design against coronavirus, style transfer and artwork generation towards machine innovation. Yet, for all the advances, modern computing systems, which rely on electronic processors, are grounded in a frustrating reality: the sheer physics of electrons restricts the computational throughput together with the chip scalability [1].

🌟 Enduring growth of neural networks' sizes for more powerful capabilities of model representation calls for considerable hardware resources. As an example, the full version of GPT-3 has a capacity of 175 billion trainable parameters, which demands over thousands of state-of-the-art NVIDIA A100 GPU cards with electricity consumption of around 5 million dollars [2]. These facts unveil important open questions as follows: How can we accelerate the artificial neural networks and promote the energy efficiency?

⚡️ Recent years have seen that integrated photonic neural networks demonstrate remarkably adept at accelerating deep neural network training and inference processes, with ultra-high speed up to $10^{12}$ multiply-accumulate operations per second [3] and ultra-low power consumption of $10^{-9}$ Watt per switching component [4]. Meanwhile, increasing technical advancements including fabrication maturity and better miniaturization are pushing the development of photonic neural networks forward at a rapid clip.

🧐 Working Principles

In the literature of optic domain, photonic neural networks (PNNs) are in essence the universal multiport interferometers. Running in a coherent manner, a vanilla PNN core contains a phase controller, several photodetectors and programmable unitary blocks. Briefly speaking, the software-defined deep neural network models are firstly recast to sets of matrix multiplications. Secondly, with the aid of singular value decomposition (SVD), the matrix operations are further reinterpreted into unitary operations, of which properties coincide with the intrinsic physics of photonic unitary components such as Mach Zehnder Interferometers (MZIs). By fine-tuning the phase shifting via phase controllers according to the aforementioned unitary operations, we finally deploy the neural networks onto our devised PNN chips.

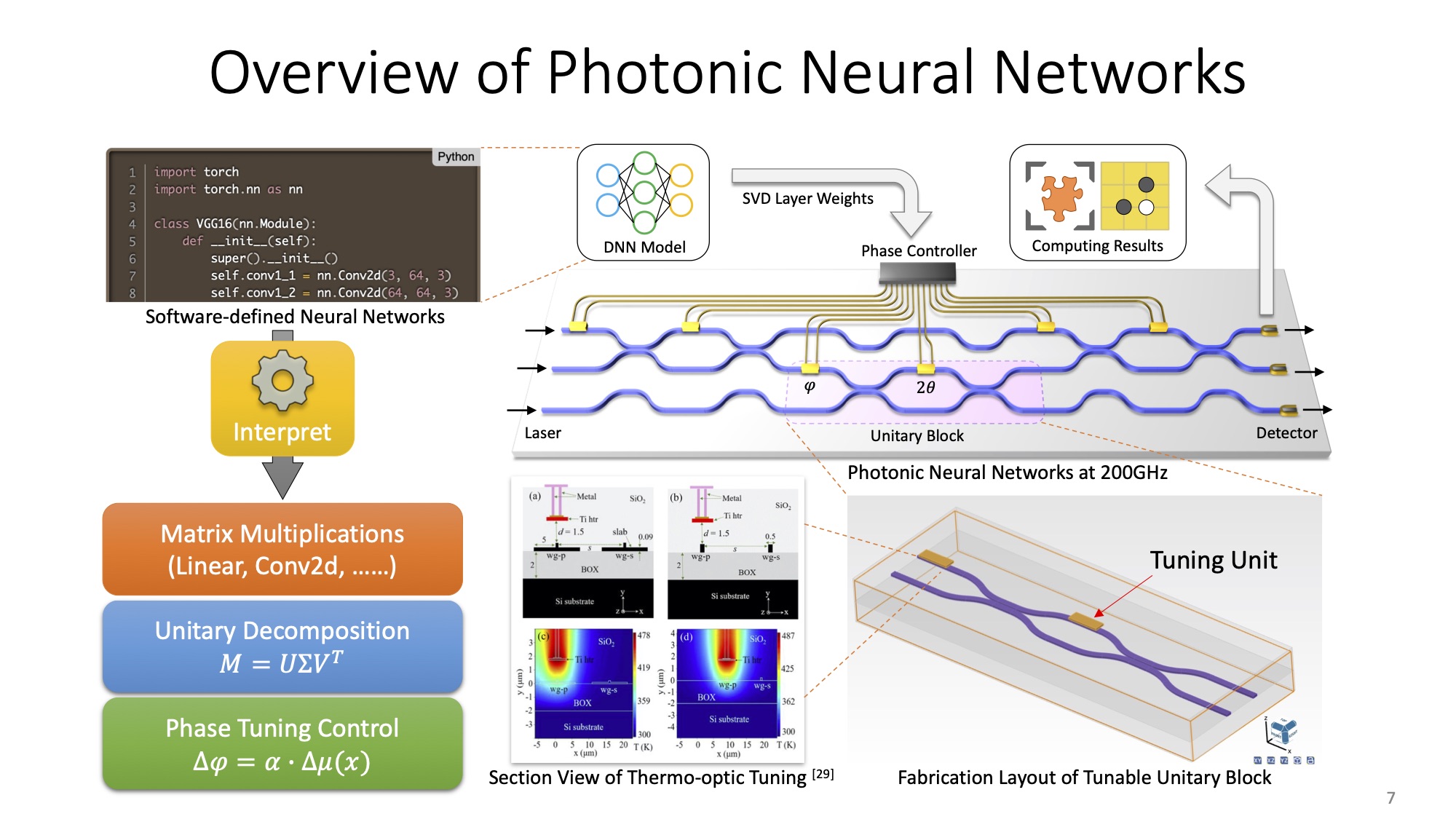
The lines in blue color denote the optical waveguide. The blocks in yellow over waveguide denote the tuning units, for example, heaters for thermo-optic modulation. I will elucidate the overall workflow from a bottom-up approach in the following sections.

🟠 Unitary Block

Unitary blocks serve as the unitary operators to manipulate the photon through the waveguide. A rough explanation of unitary is to rotate a vector without altering its amplitude. As shown in the figure below, a 2-mode unitary block of 2 inputs and 2 outputs can represent a $2 \times 2$ unitary matrix. By applying different heating power to the tuning units, we can determine the phase shift $\phi$ and $\theta$ of such the thermo-optic unitary block. Therefore, the input light of vector $[1~0]^T$ are transformed to the output vector $\left[\frac{\sqrt{3}}{2}~\frac{1}{2}\right]^T$ by way of the unitary block.

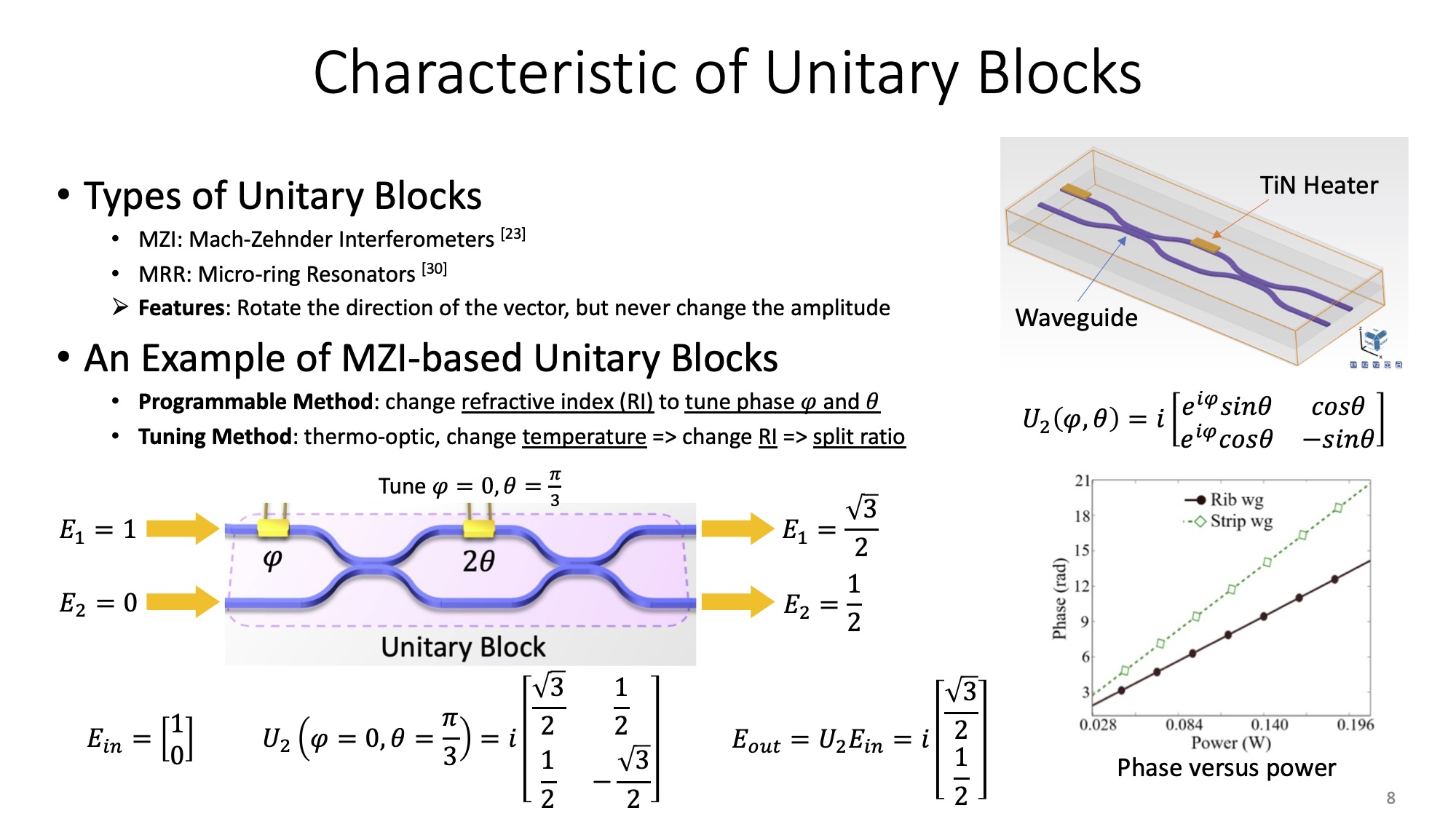
Let's look deeper into a 2-degree unitary matrix. Equation 1 shows the equivalent expression of an ideal MZI unitary block. (N-degree suggests the N-by-N unitary matrix)

$U_2(\phi, \theta) = i\begin{bmatrix}e^{i\phi}sin\theta & cos\theta \\ e^{i\phi}cos\theta & -sin\theta\end{bmatrix}\tag{1}$

But how to derive this formula? One MZI can be dissected into two phase shifters and two couplers. We adopt the form of matrix optics to represent these components.

A lossless phase shifter, which imposes the effect only at the upper bus of two parallel waveguide, is defined as Equation 2, where $\Theta$ can be $\phi$ and $2\theta$, respectively.

$M_{ps} = \begin{bmatrix} e^{i\Theta} & 0 \\ 0 & 1 \end{bmatrix}\tag{2}$

The transfer matrix of a 3dB coupler under linear optic assumption is defined as Equation 3. To put it differently, 3dB is the same as 50:50 split ratio (light intensity). The imaginary part $i$ indicates a $\frac{\pi}{2}$ phase change induced by the evanescent coupling across the materials of refractive index contrast between waveguide core and cladding.

$M_{cp} = \frac{\sqrt{2}}{2} \begin{bmatrix} 1 & i \\ i & 1 \end{bmatrix}\tag{3}$

Consequently, the overall transfer matrix of the unitary block is as Equation 4. Note that the transfer matrices of each component are left-multipled to the overall matrix in the order of light traversal.

$U_2(\phi, \theta) = M_{cp} M_{ps}(2\theta) M_{cp} M_{ps}(\phi) \tag{4}$

Nevertheless, two phase parameters also deserve careful discussion. In fact, for a real-value matrix, $\phi$ is dispensable since $\theta$ itself can cover the unitary completeness. As we are towards quantum photonics, a matrix is not necessarily all real. Thus, $\phi$ is introduced to fulfill the domain of complex region. As opposed to the $\theta$ can be continuous in $[0, 2\pi)$, the value of $\phi$ is discrete, which is one choice of $0, \frac{\pi}{2}, \pi, \frac{3\pi}{2}$. Recent works also demonstrate exploiting $\phi$ as a redundant tuning unit to suppress the process or thermal variation.

🟡 Matrix Decomposition

So far, we have learned how a 2-degree unitary block U(2) works, yet what about N-degree unitary matrices U(N) where $N > 2$? Hence, this section focuses on eking out the derivation of using several pieces of U(2) to reconstruct a U(N).

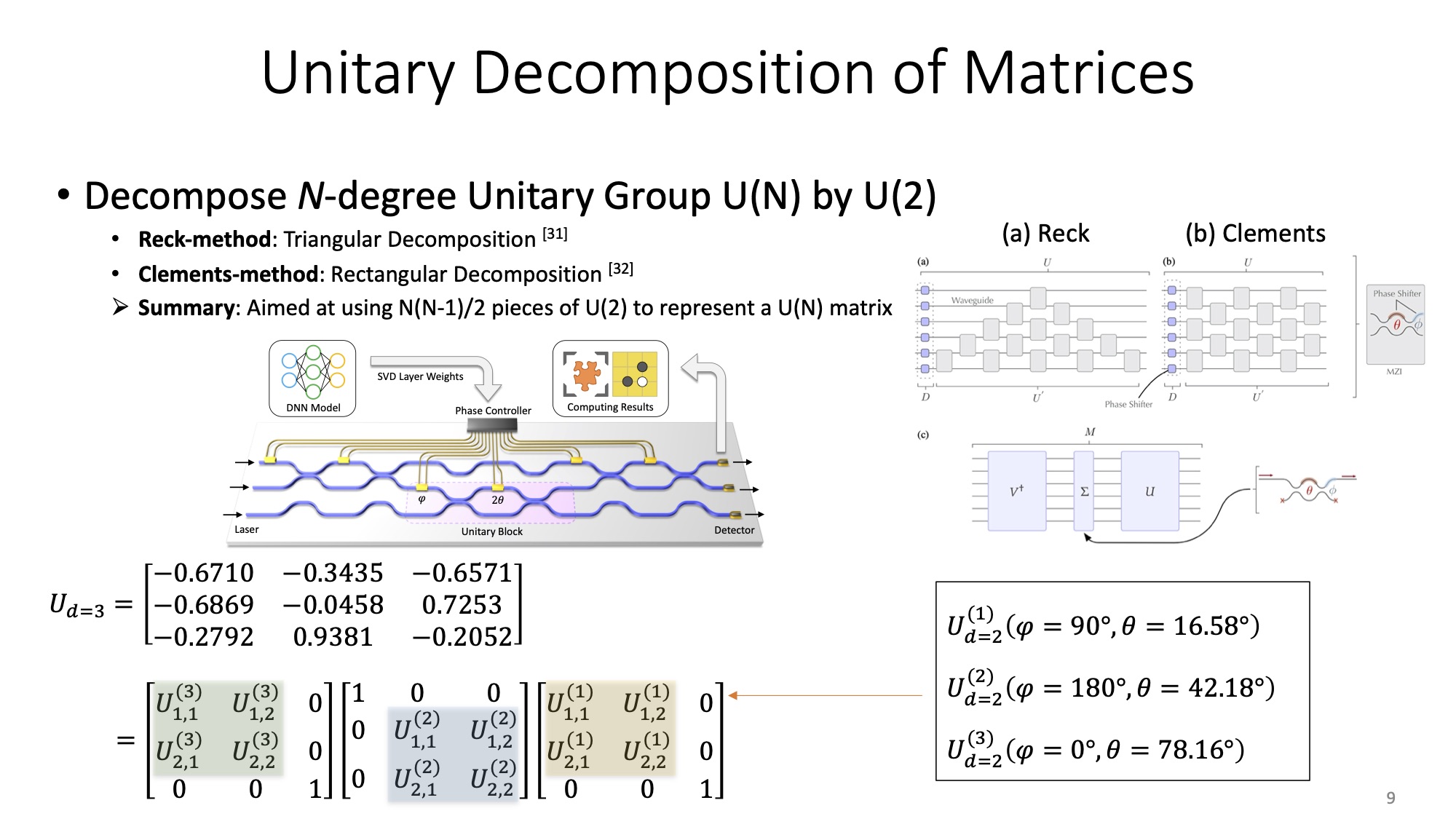
Any unitary matrices can be transformed from the identity matrix. To impose a unitary transformation on $m$-th and $n$-th port, of which symbol is defined as $T_{m,n}$ in Equation 5, it simply substitues the (m,m), (m, n), (m, n), (n, n) items of the identity matrix with those of U(2), where (m, n) indicates the $m$-th row and $n$-th column in a matrix.

$T_{m,n} = \begin{bmatrix} 1 & 0 & \cdots & 0 & 0 \\ 0 & u_{1,1} & 0 & u_{1,2} & 0 \\ \vdots & 0 & \ddots & 0 & \vdots \\ 0 & u_{2,1} & 0 & u_{2,2} & 0 \\ 0 & 0 & \cdots & 0 & 1 \end{bmatrix}\tag{5}$

Planar decomposition methods comprise Reck [5] and Clements [6]. From the mathematical perspective, Reck's method iterately right-multiplies unitary operators onto a given matrix to assemble a triangular paradigm, as shows in the slides annotation (a). By contrast, Clements' method alternately left/right multiplies unitary operators to form a rectangular paradigm, as shows in the slides annotation (b). I will start a new tutorial to illustrate the derivation of two methods in detail, but not to expand too much here. The explanation of my proposed 3D-unfolding method is also enveloped in that post.

All you need to fresh your cognition is that a U(N) can be recast into $\frac{N(N-1)}{2}$ pieces of U(2). By dedicatedly applying proper heating power onto the array of thermo-optic U(2) blocks, we can fully program the PNN chip to represent any unitary matrices as expects.

However, matrices in a real application are not necessarily unitary. We also have to seek a way to bridge the gap between arbitrary matrices and the desired unitary matrices. That's why singular value decomposition (SVD) is here.

SVD is a factorization of a real or complex matrix. It decomposes an arbitrary matrix into two unitary matrices ($U$, $V^T$) and a diagonal matrix ($\Sigma$). Unitary matrices are programmable via the aforementioned techniques. And diagonal matrices are handily mapped to either amplifiers or attenuators for the implementation. From these provisions, we successfully modulate and convey any matrices that we anticipate.

Once the setup for all tuning units is ready, such a PNN computing system is capable of obtaining matrix-vector multiplication results right after stimulation of vectorized light inputs in an ultra-low power consumption manner.

🟢 Model Reinterpretation

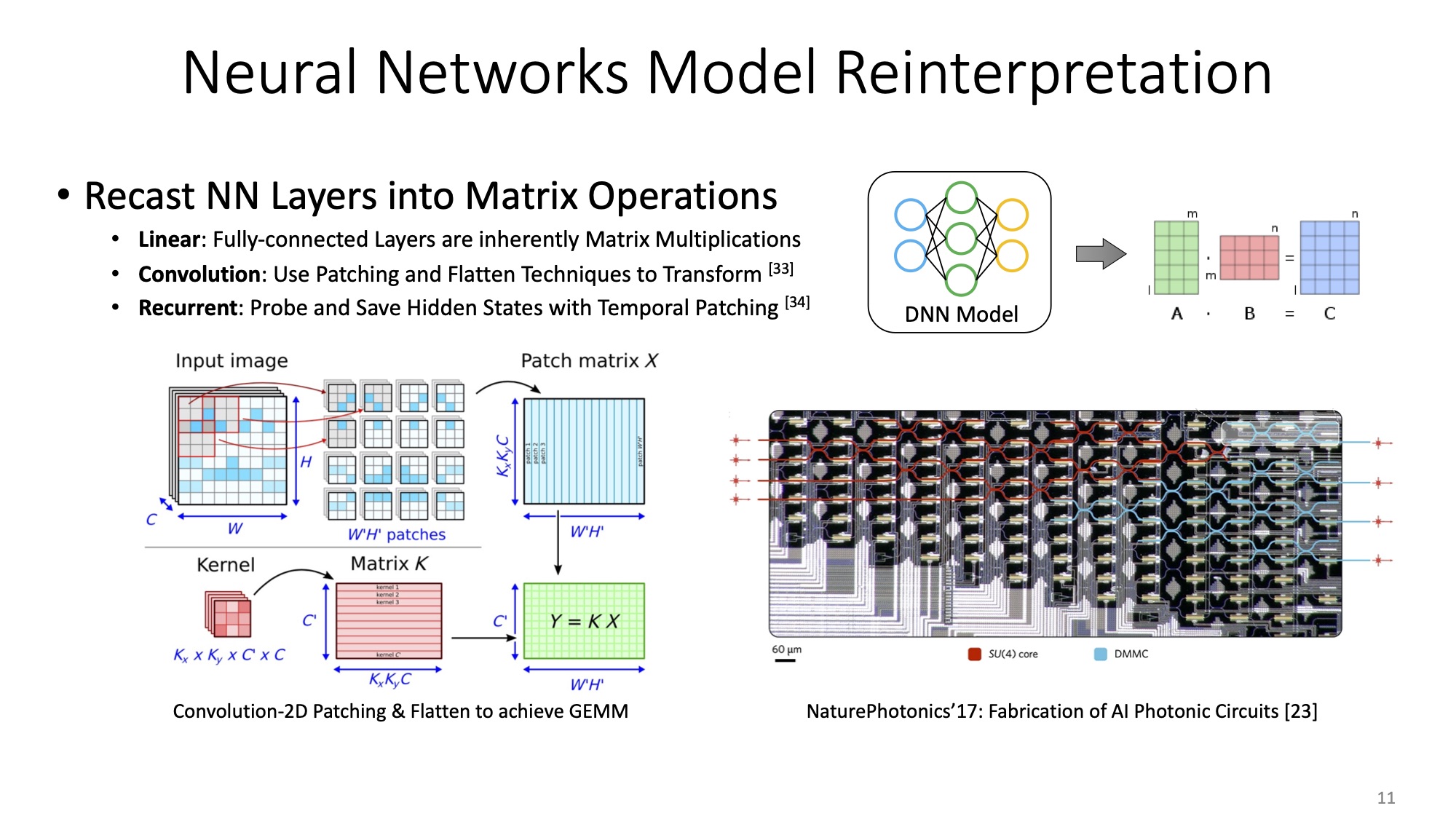
The final step is to explicitly figure out the relationship between layers within neural network models and the above-mentioned general matrix multiplications. In general, layers that cover dense matrix operations mainly comprise fully-connected layer, convolutional layer, and recurrent layer. Batch normalization, nonlinear activation and other miscellaneous layers consume way more trivial time and energy.

Linear, as known as fully-connected layer, is inherently the matrix multiplications. Conv2D is able to be reinterpreted into GEMM by patching and flatten methods. RNN shares a similar way.

🔵 Summary

Congratulation! You have gone through the fundamental idea of how to deploy and map deep neural networks onto the real photonic circuits. We generalize the workflow in a top-down approach as shows below.

⚠️ Challenges

🤔 In contrast to the digital processing in the conventional electronics, the essence of PNN is to make full use of analogue calculation. This paradigm of the aforementioned photonic computing system has proved its effectiveness. It boosts the computing density tremendously. However, this comes at a cost. In general, analogue fails in signal integrity contrarily to digital when it comes to very-large-scale (VLS) systems. To what extent users can trust the results of PNN system becomes an issue that needs urgent investigation, leading to reliability concerns. Hence, I take attempts to model and characterize the reliability of PNN in my first paper.

🤔 Another concern is that unitary blocks based on integrated Mach-Zehnder Interferometers (MZIs) require hundreds of micrometer waveguides to tune considerable phase changes. For example, the footprint of each compact MZI with a dedicated design is still over 175μm×70μm. Even a palm-sized 10cm wafer can only support a 470-port PNN, which is inadequate against the expected number of over 1000. In consideration of packaging, such a bulky PNN is definitely impractical for compact integration into edge devices. It is essential for the miniaturization of PNNs. Accordingly, I propose a 3D-unfolding method in my second paper to exploit new spatial arrangements to promote the integration density for PNN.

🤔 Let's revisit the concept of computer. The well-renowned Von Neumann architecture is essentially a processor-centric design, for the reason that the bottleneck of overall system lies on the computation part. Yet the continuing trajectory of the photonic system changes such situation. Booming improvements gained by PNN unveil the bottleneck in communication, of which bandwidth between processors and memory severely restricts the peak computational performance. This topic is enclosed in my next paper.

✅ Coming tutorials associated with my published papers will demonstrate my attempts and efforts to cross the chasm respectively!

😘 Enjoy~

📖 References

[1] Greengard, Samuel. "Photonic processors light the way." Communications of the ACM 64.9 (2021): 16-18.
[2] Brown, Tom B., et al. "Language models are few-shot learners." arXiv preprint arXiv:2005.14165 (2020).
[3] Feldmann, Johannes, et al. "Parallel convolutional processing using an integrated photonic tensor core." Nature 589.7840 (2021): 52-58.
[4] Li, Q., et al. "Ultra-power-efficient 2× 2 Si Mach-Zehnder interferometer optical switch based on III-V/Si hybrid MOS phase shifter." Optics express 26.26 (2018): 35003-35012.
[5] Reck, Michael, et al. "Experimental realization of any discrete unitary operator." Physical review letters 73.1 (1994): 58.
[6] Clements, William R., et al. "Optimal design for universal multiport interferometers." Optica 3.12 (2016): 1460-1465.