🎨 Three methods enclosed: Reck's, Clements', Yinyi's.
⭐️ An essential way to map deep neural networks onto unitary-based photonic AI circuits.

A methodology to bridge the transformation gap between the Euclidean operations in neural networks and the Hilbert operations in unitary-based photonic components.

💬 Preface

🎯 This post is of further elucidation affiliated to A Tutorial on Photonic Neural Networks, and serves to mathematically derive three decomposition methods that map matrix multiplications onto universal multiport interferometers. We also allude the theorems of matrix analysis. All the codes in this post are available on my github: Photonic-Neural-Networks.

🔑 The salient points of decomposition methods are as follows:

1. How to apply appropriate mathematical factorization;
2. How to map such mathematical conclusions onto the real physical devices.

🛫 Preliminaries

The decomposition methods listed above are component-independent. When changing the components such as from Mach Zehnder Interferometers (MZIs) to Microring Resonators (MRs), all we need is to substitute the basis that represents the targeted components before decomposing. To facilitate the comprehension, I use MZI as an example to extend the details of three decomposition methods.

🔮 Photonic Components

Let's start from the photonic components: coupler and phase shifter.

Running in a coherent manner, a coupler is defined as a transfer matrix of Equation 1, where $\kappa$ is the effective coupling coefficients of the bidirectional waveguide, and $z$ denotes the coupling length. For a 3dB coupler, which indicates a 50:50 split ratio of light intensity, $z$ is devised as $\frac{\pi}{4\kappa}$ to meet the condition $cos^2(\kappa z) = sin^2(\kappa z) = \frac{1}{2}$.

$M_{cp} = \begin{bmatrix} cos(\kappa z) & j\cdot sin(\kappa z) \\ j\cdot sin(\kappa z) & cos(\kappa z) \end{bmatrix} \tag{1}$

To make our photonic device programmable, we also need phase shifters. The phase difference incurs either constructive or destructive coherence of the light field. A phase shifter placed in the upper bus of two parallel interfere-less waveguide is defined in a matrix form, as shows in Equation 2. Phase $\theta$ is a reconfigurable variable that generalizes the alteration of refractive index (RI).

$M_{ps}(\theta) = \begin{bmatrix} e^{j\theta} & 0 \\ 0 & 1 \end{bmatrix} \tag{2}$

An MZI comprises two phase shifters and two 3dB couplers. Theoretically, two phase shifters are required to support complex matrix operations. Refer to my prior post:

Nevertheless, two phase parameters also deserve careful discussion. In fact, for a real-value matrix, $\phi$ is dispensable since $\theta$ itself can cover the unitary completeness. As we are towards quantum photonics, a matrix is not necessarily all real. Thus, $\phi$ is introduced to fulfill the domain of complex region. As opposed to the $\theta$ can be continuous in $[0, 2\pi)$, the value of $\phi$ is discrete, which is one choice of $0, \frac{\pi}{2}, \pi, \frac{3\pi}{2}$.

Therefore, the unitary basis of MZI is as Equation 3. We also entitle it a 2-degree unitary block or a U(2) block. The imaginary part $j$ suggests the $\frac{\pi}{2}$ phase change induced by evanescent coupling from low-RI to high-RI medium.

$\begin{aligned} U_2(\phi, \theta) &= M_{cp} M_{ps}(2\theta) M_{cp} M_{ps}(\phi) \\ &= j\begin{bmatrix}e^{j\phi}sin\theta & cos\theta \\ e^{j\phi}cos\theta & -sin\theta\end{bmatrix} \end{aligned} \tag{3}$

The modeling scripts in Python is composed as follows. Again, you can find the complete codes on my github with comprehensive tutorial. The parameters dim, m, n denote the dimension or degree of the overall unitary matrix, m$^{th}$ and n$^{th}$ to impose U(2), respectively. $L_p$ and $L_c$ denote the passing loss and crossing loss respectively, which will be used in fidelity analysis.

import numpy as np

def U2MZI(dim, m, n, phi, theta, Lp=1, Lc=1):
    assert m < n < dim
    mat = np.eye(dim, dtype=np.complex128)
    mat[m, m] = np.sqrt(Lp) * 1j * np.exp(1j * phi) * np.sin(theta)
    mat[m, n] = np.sqrt(Lc) * 1j * np.cos(theta)
    mat[n, m] = np.sqrt(Lc) * 1j * np.exp(1j * phi) * np.cos(theta)
    mat[n, n] = -np.sqrt(Lp) * 1j * np.sin(theta)
    return mat

🧲 Off-diagonal Nullification

Every unitary matrix is derived from the identity matrix with diagonal value of $\left[ e^{j\alpha_1}, e^{j\alpha_2} \right]^T$. We can use the arctan function to retrieve the angles that rotate, and to further determine the parameters $\phi$ and $\theta$. An example is shown in Equation 4, given an arbitrary unitary matrix $U$.

$U = \begin{bmatrix} -0.8603 & -0.5099 \\ -0.5099 & +0.8603 \end{bmatrix}\tag{4}$

The math has claimed there always exists a value of basis in Equation 3 to nullify all the off-diagonal entries of the above matrix. We pick the left-bottom value together with the right-bottom value in Equation 4, and excute arctan to recover the angle.

# Aimed at MZI block
theta = np.pi/2 - np.arctan2( np.abs(U[0, 1]), np.abs(U[1, 1]) )
phi = np.angle( U[1, 1] ) - np.angle( U[0, 1] ) + np.pi

The $U$ hereby can be reverted to identity matrix (complex). The sequences of initial offsets $\left\{ \alpha_i \right\}$ are the angle of trace of the result matrix. In this manner, we successfully calculate the parameters $\phi$ and $\theta$ of a U(2).

>>> print( u @ U2MZI(dim=2, m=0, n=1, phi, theta) )
array([[0.-1.0j, 0.-0.0j],
       [0.-0.0j, 0.-1.0j]])

Note that $U2MZI(m, n)$ is one of the implementations of $T_{m,n}$, which denotes a unitary transformation on $m^{th}$ and $n^{th}$ row. In the following sections, we will elucidate how to decompose a U(N) into $\frac{N(N-1)}{2}$ pieces of U(2) blocks by three methods respectively.

🌠 Reck's Method

Reck's method was first proposed in 1994, demonstrating on the beam splitter platform [1]. As stated before, the decomposition methods are component-independent. It is thus compatible with the basis formed by MZI.

In a nut shell, Reck's method iteratively uses the property that the product $UT^{-1}_{m,n}(\phi, \theta)$ is a unitary matrix which leaves all the columns in $U$ unaltered with the exception of columns $m$ and $n$, and we can choose values for $(\phi, \theta)$ to nullify whatever entries in these columns [4].

$U(4) = \begin{bmatrix} * & * & * & * \\ * & * & * & * \\ * & * & * & * \\ * & * & \textcolor{blue}{*} & \textcolor{red}{*} \end{bmatrix} \tag{5}$

Here we take nullifying U(4) in Equation 5 as an example. Similar to the off-diagonal nullification in the previous section, we choose a pair of $(\phi, \theta)$ for $T_{m=4, n=3}$, of which values are determined by $arctan\frac{|\textcolor{blue}{*}|}{|\textcolor{red}{*}|}$, to nullify the entries at the $4^{th}$ row and the $3^{rd}$ column of matrix U, as shows in Equation 6.

$U(4) T_{4,3}^{-1} = \begin{bmatrix} * & * & * & * \\ * & * & * & * \\ * & * & * & * \\ * & * & \textcolor{blue}{0} & \textcolor{red}{e^{j\alpha'_4}} \end{bmatrix} \tag{6}$

Nextly we iterately nullify the entire row in a descend order by column index. Refer to the property of a unitary matrix that once a given row at the $i^{th}$ index are zero except $u_{i,i}$ then all the entries in the $i^{th}$ column are also zero, the rest of the matrix after nullification is shown in Equation 7. In other words, we start from the last row, and iterately nullify entries $i$ times in the $i^{th}$ row until all the off-diagonal entries are zero.

$U(4) T_{4,3}^{-1} T_{4,2}^{-1} T_{4,1}^{-1} = \begin{bmatrix} * & * & * & \textcolor{blue}{0} \\ * & * & * & \textcolor{blue}{0} \\ * & * & * & \textcolor{blue}{0} \\ \textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{red}{e^{j\alpha_4}} \end{bmatrix} \tag{7}$

Let $R_p = \prod_{q=1}^{p-1} T_{p,q}$, Equation 7 is reformatted as $U(4) R_4$. And the rest of the workflow is as Equation 8. Additional phase shifters $\left\{ \alpha_i \right\}$ are required. Their values are the angle of trace of the result matrix: $\left\{ e^{j\alpha_i} \right\} = trace\left[ U(4) \cdot R_4 R_3 R_2 \right]$.

$U(4)R_4 R_3 R_2 = \begin{bmatrix} \textcolor{red}{e^{j\alpha_1}} & \textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{blue}{0} \\ \textcolor{blue}{0} & \textcolor{red}{e^{j\alpha_2}} & \textcolor{blue}{0} & \textcolor{blue}{0} \\ \textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{red}{e^{j\alpha_3}} & \textcolor{blue}{0} \\ \textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{red}{e^{j\alpha_4}} \end{bmatrix} \tag{8}$

For more details of the codes, please refer to my github. The APIs are listed below:

from pnn import decompose_reck, reconstruct_reck

[phi, theta, alpha] = decompose_reck(u, block='mzi')
u_r = reconstruct_reck(phi, theta, alpha, block='mzi')

🎆 Clements' Method

Clements' method is an optimized arrangement beyond Reck's, presented in 2016 [2]. It is based on an alternative arrangement of U(2) to reduce the footprint and improve the fidelity against the optical losses.

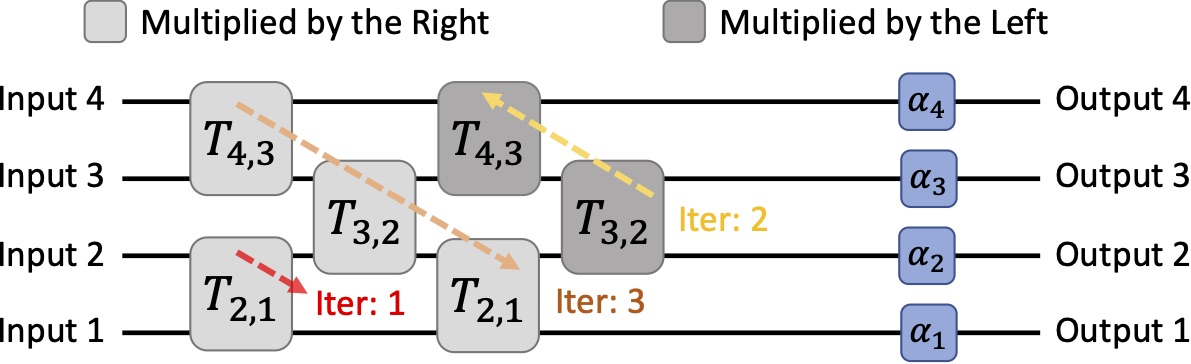
In contrast to Reck's method that successively multiply $T_{m,n}^{-1}$ unitary matrices by the right to nullify the off-diagonal entries, Clements' method proceeds by nullifying successive diagonals of U(N) by alternating between $T_{m,n}$ and $T_{m,n}^{-1}$ unitary matrices where $m=n-1$ [4]. To put it differently, $T_{m,n}$ and $T_{m,n}^{-1}$ indicate the U(2) blocks from near-output and near-input, respectively. The star in blue color is the target to nullify, and the start in red is the value that aids in nullification. Specifically, the value is associated with $arctan\frac{|\textcolor{blue}{*}|}{|\textcolor{red}{*}|}$.

$U(4) = \begin{bmatrix} * & * & * & * \\ * & * & * & * \\ * & * & * & * \\ \textcolor{blue}{*} & \textcolor{red}{*} & * & * \end{bmatrix} \tag{9}$

Let's still use U(4) as the example. As opposed to Reck's, we start to nullify the entry at the left-bottom corner. Note that $T_{m,n}^{-1}$ that multipies by the right indicates the nullification between $m^{th}$ and $n^{th}$ column, while $T_{m,n}$ that multiply by the left suggests the nullification between $m^{th}$ and $n^{th}$ row. The result is yielded in Equation 10.

$U(4)\textcolor{green}{T_{2,1}^{-1}} = \begin{bmatrix} * & * & * & * \\ \textcolor{red}{*} & * & * & * \\ \textcolor{blue}{*} & * & * & * \\ \textcolor{green}{0} & * & * & * \end{bmatrix} \tag{10}$

To traverse the entries in a zig-zag manner, we gradually nullify the entries and make it a upper triangular matrix. For the odd iterations, we apply column nullification $T_{m,n}^{-1}$. For the even iterations, we apply row nullifications $T_{m,n}$.

$\textcolor{purple}{T_{3,2}}U(4)\textcolor{green}{T_{2,1}^{-1}} = \begin{bmatrix} * & * & * & * \\ * & * & * & * \\ \textcolor{purple}{0} & \textcolor{red}{*} & * & * \\ \textcolor{green}{0} & \textcolor{blue}{*} & * & * \end{bmatrix} \tag{11}$

The result matrix is shown in Equation 12. The first iteration is $\textcolor{green}{T_{2,1}^{-1}}$. The second iteration comprises in order $\textcolor{purple}{T_{3,2}}$ and $\textcolor{cyan}{T_{4,3}}$. The third iteration comprises $\textcolor{blue}{T_{4,3}^{-1}}$, $\textcolor{red}{T_{3,2}^{-1}}$ and $\textcolor{orange}{T_{2,1}^{-1}}$.

$\textcolor{cyan}{T_{4,3}}\textcolor{purple}{T_{3,2}}U(4)\textcolor{green}{T_{2,1}^{-1}}\textcolor{blue}{T_{4,3}^{-1}}\textcolor{red}{T_{3,2}^{-1}}\textcolor{orange}{T_{2,1}^{-1}} = \begin{bmatrix} * & * & * & * \\ \textcolor{orange}{0} & * & * & * \\ \textcolor{purple}{0} & \textcolor{red}{0} & * & * \\ \textcolor{green}{0} & \textcolor{cyan}{0} & \textcolor{blue}{0} & * \end{bmatrix} \tag{12}$

Note that the alternative form of $D=\textcolor{cyan}{T_{4,3}}\textcolor{purple}{T_{3,2}}U(4)\textcolor{green}{T_{2,1}^{-1}}\textcolor{blue}{T_{4,3}^{-1}}\textcolor{red}{T_{3,2}^{-1}}\textcolor{orange}{T_{2,1}^{-1}}$ is not friendly to the reconstruction. We are supposed to move all the transform unitary matrices $T$ to either left side $T_{m,n}$ or right side $T_{m,n}^{-1}$. Therefore, Equation 12 needs further reordering to yield the final form as Equation 13. $D''$ is for reconstruction.

$\begin{aligned} U(4) &= \textcolor{purple}{T_{3,2}^{-1}}\textcolor{cyan}{T_{4,3}^{-1}}D\textcolor{orange}{T_{2,1}}\textcolor{red}{T_{3,2}}\textcolor{blue}{T_{4,3}}\textcolor{green}{T_{2,1}} \\ &= \textcolor{purple}{T_{3,2}^{-1}}D'\textcolor{cyan}{T_{4,3}}\textcolor{orange}{T_{2,1}}\textcolor{red}{T_{3,2}}\textcolor{blue}{T_{4,3}}\textcolor{green}{T_{2,1}} \\ &= D''\textcolor{purple}{T_{3,2}}\textcolor{cyan}{T_{4,3}}\textcolor{orange}{T_{2,1}}\textcolor{red}{T_{3,2}}\textcolor{blue}{T_{4,3}}\textcolor{green}{T_{2,1}} \end{aligned} \tag{13}$

The derivation from $D$ to $D''$ is demonstrated as Equation 14, where $\alpha=\frac{n}{2}\pi; n=0, 1, 2, 3$. To simplify the forms of the ensuing equations, we define $a=e^{j\alpha}$.

$D=\begin{bmatrix} e^{j\alpha_1} & 0 \\ 0 & e^{j\alpha_2} \end{bmatrix} \tag{14}$

Let $T_{m,n}^{-1}(\phi,\theta)D=D'T_{m,n}(\phi',\theta')$, all the entries should match. By virtue of the properties of trigonometric functions, one of situations that meet the formula below are $\theta=\theta'$ to suppress all the cosine and sine terms.

The simplified results are shown in Equation 15 in the ensuing fashion. By moving $T_{m,n}$ to the right of $D$ consecutively, it yields $U = D'\prod T_{m,n}^{-1}$ as expects. $D'$ contains the values of $\{\alpha_i\}$.

$\begin{aligned} a_1 &= a_1'e^{j(\phi+\phi')} \\ a_1' &= -a_2 e^{-j\phi} \end{aligned} \tag{15}$

For more details of the codes, please refer to my github. The APIs are listed below:

from pnn import decompose_clements, reconstruct_clements

[phi, theta, alpha] = decompose_clements(u, block='mzi')
u_r = reconstruct_clements(phi, theta, alpha, block='mzi')

🎇 Yinyi's Method

I present a 3D-unfolding method to dramatically enhance computational density as we are towards miniaturization practice of photonic neural networks for Internet of Thing [3].

🚴 Motivation

Integrated photonic neural networks, which are based on universal multiport interferometers (UMI), have already evolved from hype to reality over past few years. A fairly solid foundation of working mechanism, continuing progress ranging from fabrication maturities to algorithm advances push universal multiport interferometers forward. Some startup commanies have aggressively taped out wafer-scale photonic chips for datacenters.

Despite the great potentials mentioned above, such photonic paradigms have not yet delivered on the promises in miniaturization practice. In general, the footprints of photonic components are several orders of magnitudes larger than those of electronic devices. For instance, the length of an arm in MZI is over hundreds of micrometers. A planar arrangement, by either Reck's or Clements', to support $256\times 256$ matrix multiplications on multiport interferometers will occupy a whole 4-inch wafer. The horribly large size impedes the integration of such photonic neural networks into mobile devices and other agile apparatuses, which literally extinguishes the prospects for AI in Internet of Thing with Photonics.

It is therefore imperative to reduce the footprints and improve the computational density. Remind that Reck's and Clements' are both planar decomposition, will it be possible to explore the optimal 3D arrangement for unitary blocks? The answer is YES. Here we propose a novel 3D-unfolding method based on cosine-sine decomposition (CSD).

💡 Methodology

As a starting point, we mathematically investigate the properties of CSD. We begin with a weight matrix $W$ obtained from the layer of a deep neural network model. Typically, the weight matrix is mapped to unitary domain via Singular Value Decomposition (SVD), that is $W=U\Sigma V$. It yields two orthogonal matrices $U$ and $V$. For simplicity, we use M to represent either U or V as the input matrix at a single execution of our unfolding method. Each unitary matrix $M$ is partitioned into four sub-matrices with the size of $p\times p$, $p\times (n-p)$, $(n-p)\times p$ and $(n-p)\times (n-p)$. Here $p$ and its remainders $n-p$ straightforward determine the planar scales of UMI at each layer. Since the overall footprints are subject to the largest area among layers, the value of $p$ should be as close to that of $n-p$ as possible to make balance unfolding. Empirically, $p = n/2$ when $n$ is even, and $p = (n − 1)/2$ when $n$ is odd.

$M_{n\times n} = \begin{bmatrix} M_{1,1} & M_{1,2} \\ M_{2,1} & M_{2,2} \end{bmatrix}$

For the next step, we apply CSD to $M$ with balanced parameters of $p$ as stated. There exists orthogonal matrices $U_1, U_2 \in \mathcal{R}^{p\times p}$, $V_1, V_2 \in \mathcal{R}^{(n-p)\times (n-p)}$ and diagonal matrices comprosed of trigonometric $C$, $S$. The entire formula is as follows:

$I$ denotes an identity matrix, and $c_i^2 + s_i^2=1$ holds for any corresponding entries of $C$ and $S$. For each pair of $c_i$ and $s_i$, they indicate a vertical coupling block. By contrast, $U$ and $V$ are the planar or horizontal coupling in a way like Reck's or Clements'. It suggests our method is fully compatible with two canonical methods, while further enabling the arrangement along the direction that is perpendicular to the plane.

The illustration of the CSD-based unfolding method for a $4\times 4$ UMI is depicted below. We get down to Clements' planar decomposition method a a baseline in sub-figure (a). It represents a $4\times 4$ unitary matrix $M$. Before CS-decomposition, $M$ is evenly partitioned into four sub-matrix blocks in green color shown in sub-figure (b). Note that the colors of matrices correspond to the waveguide mesh colors in the subfigure (c) and (d). To reconstruct each layer PNNs from the unfolding sub-matrices, the $U$ and $V$ correspond to the planar waveguide mesh. The black arrow-lines suggest that inter-layer $C$ and $S$ share resemble ports and structures, which can be amalgamated along the vertical direction. We hereby complete a single execution of CSD.

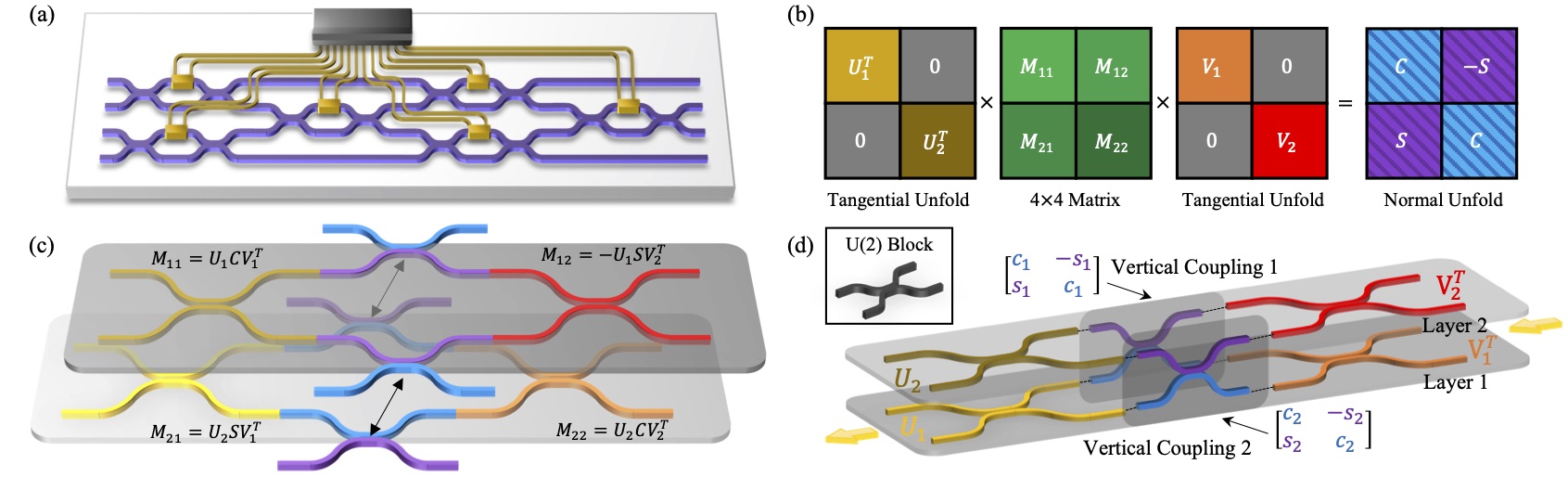
Since the sub-matrices $U$ and $V$ still maintain the consistency of unitary properties, our CSD method can iteratively apply to the rest of the sub-matrices and achieve multi-layer stacking along the plane normal. In addition, the method is highly customizable in terms of the vertical stacking number. From the perspective of the algorithm, that each unitary matrix is decomposed into two sub-matrices is associated with the binary tree. By specifying the tree depth, the numbers of vertical layers are determined.

For more details of the codes, please refer to my github. The APIs are listed below:

class UmiCsd:
    def decompose(matrix, p=None, q=None) -> None
    def decompose_recursive(depth) -> None
    def reconstruct(Lp_dB=0, Lc_dB=0, method='clements', block='bs') -> numpy.ndarray

The method in UmiCsd.reconstruct() denotes the planar decomposition method, including Reck or Clements. In summary, our proposed CSD method is compatible with Reck's and Clements' method, while ours enables spatial arrangement along new axis to reduce the footprint areas.

🗯 Discussion

FAQ: Why not simply stacking each planar layers without vertical coupling? The fabrication process seems more viable.

It is important to recognize the defects of photonic systems before we move on. A commonsense is that buffering or storage is extremely expensive in the photonic system due to the intrinsic properties of photons. Moreover, to pursue ultra-low power consumption, the devised system is supposed to avoid frequent optical-to-electrical (OE) conversions and vice versa.

And let's back to the question. The arithmetic operations behind stacking each planar layers without vertical coupling actually, which are in essence tiled multiplications, are NOT equivalent to those of our method. Simply stacking calculates each sub-matrice as tiles individually, and the results of output ports between layers are mutually independent. To acquire the final results, we still need extra components of either photonic buffers or intra-mesh OE conversions to store, synchronize and accumulate the partial sum produced from tiles. As stated in the last paragraph, these devices are not impractical for photonic systems.

Futhermore, even if we argument simply stacking by attaching vertical coupling to avoid buffering and intra-mesh OE conversions, our CSD is the optimal design with respect to both the fidelity and footprints.

🧐 Comparison

📐 Fidelity

🔩 Footprint

📝 Conclusion

📖 References

[1] Reck, Michael, et al. "Experimental realization of any discrete unitary operator." Physical review letters 73.1 (1994): 58.
[2] Clements, William R., et al. "Optimal design for universal multiport interferometers." Optica 3.12 (2016): 1460-1465.
[3] Liu, Yinyi, et al. "Reduce footprints of multiport interferometers by cosine-sine-decomposition unfolding." Optical Fiber Communication Conference and Exhibition (2022): W2A.4.
[4] Pérez, Daniel, et al. "Principles, fundamentals, and applications of programmable integrated photonics." Advances in Optics and Photonics 12.3 (2020): 709-786.